[DSA] Độ phức tạp thuật toán

Nguồn: Click here

1. Độ phức tạp thuật toán là gì?

Độ phức tạp thuật toán (algorithm complexity) là một khái niệm trong khoa học máy tính, đo lường độ khó của một thuật toán để giải quyết một vấn đề. Nó được đo bằng cách xác định số lần thực hiện một lệnh hoặc số lần truy cập đến một giá trị trong thuật toán, dựa trên kích thước đầu vào.

Có hai loại độ phức tạp thuật toán chính:

1.1. Độ phức tạp thời gian: 

Độ phức tạp thời gian của một thuật toán là số lần thực hiện các phép tính cơ bản, như phép so sánh, phép toán số học, phép gán, v.v., dựa trên kích thước của dữ liệu đầu vào. Độ phức tạp thời gian được đo bằng số lần thực hiện các phép tính tương ứng với kích thước đầu vào.

1.2. Độ phức tạp không gian: 

Độ phức tạp không gian của một thuật toán là số lượng bộ nhớ cần thiết để lưu trữ dữ liệu và thông tin trung gian trong quá trình thực hiện thuật toán, dựa trên kích thước của dữ liệu đầu vào. Độ phức tạp không gian được đo bằng số lượng bộ nhớ cần thiết để lưu trữ dữ liệu và thông tin trung gian tương ứng với kích thước đầu vào.

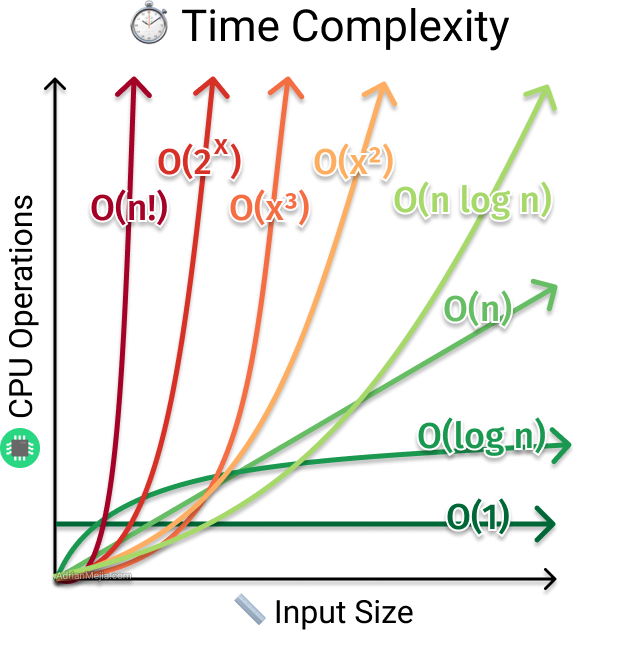
Các loại độ phức tạp thuật toán thường được biểu diễn bằng các ký hiệu toán học như O(n), O(n^2), O(log n), v.v. ở đó n là kích thước của dữ liệu đầu vào. Các ký hiệu này cho biết mức độ tăng trưởng của độ phức tạp thuật toán khi kích thước của dữ liệu đầu vào tăng lên. Ví dụ: O(n) đại diện cho độ phức tạp thuật toán tuyến tính, trong khi O(n^2) đại diện cho độ phức tạp thuật toán bậc hai.

2. Ví dụ về độ phức tạp thuật toán:

Giả sử chúng ta có một mảng số nguyên có kích thước n, và chúng ta muốn tìm số lớn nhất trong mảng đó. Ta có thể giải quyết bài toán này bằng cách duyệt qua từng phần tử trong mảng và so sánh giá trị của phần tử đó với giá trị số lớn nhất hiện tại. Nếu giá trị của phần tử đó lớn hơn giá trị số lớn nhất hiện tại, chúng ta cập nhật giá trị số lớn nhất hiện tại bằng giá trị của phần tử đó.

Độ phức tạp thời gian của thuật toán này là O(n), vì chúng ta cần duyệt qua từng phần tử trong mảng một lần. Nếu kích thước của mảng tăng lên, thời gian thực hiện thuật toán cũng tăng theo tỉ lệ tuyến tính.

Độ phức tạp không gian của thuật toán này là O(1), vì chúng ta chỉ cần lưu trữ hai biến số lớn nhất hiện tại và chỉ số của phần tử số lớn nhất. Không có bất kỳ cấu trúc dữ liệu hay mảng bổ sung nào được sử dụng để lưu trữ dữ liệu hoặc thông tin trung gian, vì vậy không có sự tăng trưởng không gian khi kích thước của mảng tăng lên.

Đây là một ví dụ đơn giản về độ phức tạp thuật toán. Việc hiểu và tính toán độ phức tạp thuật toán là rất quan trọng trong thiết kế và phân tích thuật toán để đảm bảo hiệu quả và hiệu suất tối ưu.

3. Một số thuật toán cơ bản và độ phức tạp của nó:

3.1. Thuật toán tìm kiếm tuyến tính (Linear Search):

• Độ phức tạp thời gian: O(n)
• Độ phức tạp không gian: O(1)

 Thuật toán tìm kiếm tuyến tính là một thuật toán đơn giản và dễ hiểu, được sử dụng để tìm kiếm một phần tử trong một mảng. Cách thức hoạt động của thuật toán này là duyệt lần lượt từng phần tử của mảng cho đến khi tìm được phần tử cần tìm, hoặc đến khi duyệt hết mảng mà vẫn không tìm thấy.

• Độ phức tạp thời gian của thuật toán tìm kiếm tuyến tính là O(n), với n là số lượng phần tử trong mảng. Nghĩa là, thời gian thực hiện thuật toán tăng tỉ lệ trực tiếp với kích thước của dữ liệu đầu vào. Ví dụ, nếu mảng có 100 phần tử, thì thuật toán tìm kiếm tuyến tính sẽ duyệt qua toàn bộ 100 phần tử để tìm kiếm phần tử cần tìm.
• Độ phức tạp không gian của thuật toán tìm kiếm tuyến tính là O(1), vì chỉ cần sử dụng một biến đếm để duyệt mảng và không cần lưu trữ bất kỳ thông tin nào khác.

Tuy nhiên, mặc dù thuật toán tìm kiếm tuyến tính đơn giản, nhưng độ phức tạp của nó là khá lớn. Đặc biệt là khi mảng có kích thước lớn, thì thời gian thực hiện thuật toán sẽ rất chậm và không hiệu quả. Do đó, khi có nhiều phương án để tìm kiếm trong mảng, ta nên xem xét sử dụng các thuật toán tìm kiếm khác với độ phức tạp thấp hơn để tăng tốc độ thực hiện và hiệu quả của chương trình.

3.2. Thuật toán tìm kiếm nhị phân (Binary Search):

• Độ phức tạp thời gian: O(log n)
• Độ phức tạp không gian: O(1)

 Thuật toán tìm kiếm nhị phân là một thuật toán hiệu quả được sử dụng để tìm kiếm một phần tử trong một mảng đã được sắp xếp theo thứ tự tăng dần hoặc giảm dần. Thuật toán này hoạt động bằng cách tìm kiếm phần tử ở giữa mảng, so sánh giá trị của nó với giá trị cần tìm và loại bỏ một nửa mảng không cần thiết, lặp lại quá trình tìm kiếm này cho đến khi tìm được phần tử cần tìm hoặc xác định rằng phần tử không tồn tại trong mảng.

• Độ phức tạp thời gian của thuật toán tìm kiếm nhị phân là O(log n), với n là số lượng phần tử trong mảng. Nghĩa là, thời gian thực hiện thuật toán không tăng tỉ lệ trực tiếp với kích thước của dữ liệu đầu vào, mà chỉ tăng theo cấp số nhân. Ví dụ, nếu mảng có 100 phần tử, thì thuật toán tìm kiếm nhị phân chỉ cần tối đa log₂(100) = 6 lần tìm kiếm để tìm được phần tử cần tìm.
• Độ phức tạp không gian của thuật toán tìm kiếm nhị phân là O(1), vì chỉ cần sử dụng một vài biến để lưu trữ thông tin như chỉ số phần tử trung tâm của mảng, không cần sử dụng thêm bộ nhớ để lưu trữ dữ liệu khác.

Với độ phức tạp thấp hơn nhiều so với thuật toán tìm kiếm tuyến tính, thuật toán tìm kiếm nhị phân là một trong những thuật toán tìm kiếm hiệu quả nhất và được sử dụng rộng rãi trong các ứng dụng và các hệ thống lớn. Tuy nhiên, để áp dụng thuật toán này, mảng phải được sắp xếp trước đó, điều này cũng đòi hỏi một độ phức tạp để thực hiện việc sắp xếp mảng.

3.3. Thuật toán sắp xếp chọn (Selection Sort):

• Độ phức tạp thời gian: O(n^2)
  Độ phức tạp không gian: O(1)

Thuật toán sắp xếp chọn (selection sort) là một trong những thuật toán đơn giản nhất để sắp xếp một danh sách. Các bước thực hiện của thuật toán sắp xếp chọn là:

• Tìm phần tử nhỏ nhất trong danh sách.
• Hoán đổi phần tử nhỏ nhất với phần tử đầu tiên trong danh sách.
• Tìm phần tử nhỏ nhất trong danh sách con từ vị trí thứ hai đến hết danh sách.
• Hoán đổi phần tử nhỏ nhất với phần tử thứ hai trong danh sách.
• Tiếp tục thực hiện cho đến khi toàn bộ danh sách đã được sắp xếp.

Độ phức tạp của thuật toán sắp xếp chọn là O(n^2), trong đó n là số lượng phần tử trong danh sách. Thuật toán này phải duyệt qua toàn bộ danh sách nhiều lần để tìm kiếm phần tử nhỏ nhất và hoán đổi vị trí các phần tử, do đó số lần lặp lại của thuật toán tăng theo cấp số nhân khi kích thước danh sách tăng lên.

Vì vậy, với danh sách có số lượng phần tử lớn, thuật toán sắp xếp chọn trở nên chậm và không phù hợp với việc sắp xếp các danh sách lớn. Tuy nhiên, đối với những danh sách nhỏ và đã được sắp xếp một phần, thuật toán sắp xếp chọn vẫn là lựa chọn tốt.

3.4. Thuật toán sắp xếp nhanh (Quick Sort):

• Độ phức tạp thời gian trung bình: O(n log n)
• Độ phức tạp thời gian tệ nhất: O(n^2)
• Độ phức tạp không gian: O(log n)

Thuật toán sắp xếp nhanh (Quick Sort) là một trong những thuật toán sắp xếp hiệu quả nhất và được sử dụng rộng rãi. Thuật toán sắp xếp nhanh hoạt động dựa trên phương pháp chia để trị, tìm một phần tử đại diện (pivot) rồi chia dãy thành 3 phần là dãy bé hơn pivot, dãy lớn hơn pivot và dãy có giá trị bằng pivot. Tiếp tục áp dụng phương pháp chia để trị đối với hai phần tử bé hơn và lớn hơn pivot cho đến khi dãy chỉ còn một phần tử hoặc không có phần tử nào cần sắp xếp.

Cụ thể, thuật toán sắp xếp nhanh có các bước thực hiện như sau:

• Chọn một phần tử đại diện (pivot) từ danh sách.
• Phân vùng (partition) danh sách thành ba phần: danh sách bé hơn pivot, danh sách lớn hơn pivot và danh sách có giá trị bằng pivot.
• Sử dụng đệ quy để sắp xếp danh sách bé hơn pivot và danh sách lớn hơn pivot.

Độ phức tạp của thuật toán sắp xếp nhanh là O(nlog(n)) trong trường hợp trung bình và tốt nhất, và O(n^2) trong trường hợp xấu nhất. Trong trường hợp tốt nhất và trung bình, thuật toán sắp xếp nhanh có thể sắp xếp danh sách nhanh chóng với độ phức tạp O(nlog(n)). Tuy nhiên, trong trường hợp xấu nhất, khi pivot luôn là phần tử lớn nhất hoặc bé nhất trong danh sách, thuật toán sẽ hoạt động với độ phức tạp O(n^2), điều này khiến thuật toán trở nên chậm và không hiệu quả.

Để tối ưu hiệu suất của thuật toán sắp xếp nhanh, ta có thể lựa chọn pivot sao cho phần tử đại diện này là phần tử trung vị của danh sách, hoặc sử dụng các kỹ thuật tối ưu khác để giảm thiểu trường hợp xấu nhất của thuật toán.

3.5. Thuật toán sắp xếp trộn (Merge Sort):

• Độ phức tạp thời gian: O(n log n)
• Độ phức tạp không gian: O(n)

Thuật toán sắp xếp trộn (Merge Sort) có độ phức tạp là O(n log n) trong trường hợp trung bình và trong trường hợp tốt nhất và tệ nhất cũng là O(n log n).

Thuật toán sắp xếp trộn là một thuật toán chia để trị, nghĩa là nó chia một mảng lớn thành hai mảng con cùng kích thước (hoặc gần như bằng nhau), tiếp đó sắp xếp từng mảng con bằng cách đệ quy, và sau đó trộn hai mảng đã sắp xếp thành một mảng đã sắp xếp lớn hơn.

Trong quá trình trộn, thuật toán duyệt qua từng phần tử của hai mảng và so sánh chúng để đưa vào mảng kết quả theo thứ tự. Điều này yêu cầu độ phức tạp thời gian của thuật toán là O(n), trong đó n là tổng số phần tử của hai mảng. Vì mảng ban đầu được chia đôi liên tiếp cho đến khi chỉ còn một phần tử, do đó số lần trộn sẽ là log n. Vì vậy, tổng độ phức tạp thời gian của thuật toán sắp xếp trộn sẽ là O(n log n).

3.6. Thuật toán tìm kiếm đường đi ngắn nhất (Shortest Path Algorithm):

• Độ phức tạp thời gian: O(E log V), với E là số lượng cạnh và V là số lượng đỉnh trong đồ thị.
  Độ phức tạp không gian: O(V)

Thuật toán tìm kiếm đường đi ngắn nhất (Shortest Path Algorithm) có nhiều biến thể khác nhau, trong đó thuật toán Dijkstra và thuật toán Bellman-Ford là hai thuật toán phổ biến. Độ phức tạp của hai thuật toán này khác nhau.

3.6.1. Thuật toán Dijkstra

Thuật toán Dijkstra sử dụng một cấu trúc dữ liệu hàng đợi ưu tiên (priority queue) để duyệt các đỉnh trong đồ thị theo thứ tự đường đi ngắn nhất. Độ phức tạp của thuật toán Dijkstra là O((V+E)logV), trong đó V là số đỉnh và E là số cạnh của đồ thị.

Trong quá trình duyệt đồ thị, thuật toán Dijkstra sử dụng hàng đợi ưu tiên để lưu trữ các đỉnh cần xét. Mỗi lần lấy ra đỉnh có đường đi ngắn nhất từ đỉnh nguồn, ta cập nhật lại các đường đi đến các đỉnh kề với đỉnh đó. Quá trình này tiếp tục cho đến khi tất cả các đỉnh trong đồ thị được duyệt.

3.6.2. Thuật toán Bellman-Ford

Thuật toán Bellman-Ford sử dụng một mảng để lưu trữ đường đi ngắn nhất từ đỉnh nguồn đến mỗi đỉnh trong đồ thị. Mảng này được cập nhật sau mỗi lần duyệt toàn bộ các cạnh của đồ thị. Độ phức tạp của thuật toán Bellman-Ford là O(VE), trong đó V là số đỉnh và E là số cạnh của đồ thị.

Trong quá trình duyệt đồ thị, thuật toán Bellman-Ford duyệt toàn bộ các cạnh của đồ thị V-1 lần. Mỗi lần duyệt, thuật toán cập nhật lại đường đi ngắn nhất đến mỗi đỉnh. Sau V-1 lần duyệt, thuật toán kiểm tra xem có chu trình âm trong đồ thị hay không. Nếu có, thuật toán trả về một thông báo cho biết không thể tìm được đường đi ngắn nhất. Nếu không có chu trình âm, thuật toán trả về đường đi ngắn nhất từ đỉnh nguồn đến mỗi đỉnh trong đồ thị.

Tóm lại, độ phức tạp của thuật toán tìm kiếm đường đi ngắn nhất phụ thuộc vào thuật toán được sử dụng và đặc tính của đồ thị.

3.7. Thuật toán cây tìm kiếm nhị phân (Binary Search Tree):

• Độ phức tạp thời gian trung bình: O(log n)
• Độ phức tạp không gian: O(n)

Độ phức tạp của các thao tác trong cây tìm kiếm nhị phân (Binary Search Tree - BST) được tính theo chiều cao của cây. Vì vậy, để tính độ phức tạp trung bình của các thao tác, ta cần xác định chiều cao trung bình của cây.

Trong trường hợp tốt nhất, khi cây được cân bằng, chiều cao của cây là log2(n), n là số lượng nút trong cây. Trong trường hợp xấu nhất, cây có thể trở thành một danh sách liên kết, khi đó chiều cao của cây là n.

Các thao tác cơ bản trong BST bao gồm: tìm kiếm, thêm và xóa một nút.

• Tìm kiếm: Độ phức tạp của tìm kiếm trong BST là O(log2(n)) trong trường hợp tốt nhất và O(n) trong trường hợp xấu nhất, nếu cây trở thành một danh sách liên kết.
• Thêm: Độ phức tạp của việc thêm một nút vào BST cũng tương tự như tìm kiếm, trong trường hợp tốt nhất và trung bình là O(log2(n)), trong trường hợp xấu nhất là O(n).
• Xóa: Độ phức tạp của việc xóa một nút từ BST phụ thuộc vào chiều cao của cây. Trong trường hợp tốt nhất và trung bình, độ phức tạp là O(log2(n)), trong trường hợp xấu nhất là O(n).

Vì vậy, việc duy trì một BST cân bằng rất quan trọng để đảm bảo độ phức tạp tốt nhất trong việc thực hiện các thao tác trên BST. Các phương pháp cân bằng BST phổ biến bao gồm cây đỏ-đen (red-black tree) và cây AVL.

4. Kết luận

Độ phức tạp của một thuật toán phụ thuộc vào nhiều yếu tố, bao gồm kích thước đầu vào, cách sắp xếp và phân chia dữ liệu, và các hoạt động cơ bản được sử dụng để giải quyết bài toán. Hiểu rõ độ phức tạp của các thuật toán sẽ giúp chúng ta lựa chọn và sử dụng chúng một cách hiệu quả hơn.

Nguồn: chatGPT