[DSA] Cấu trúc dữ liệu Stack

1. Stack là gì?

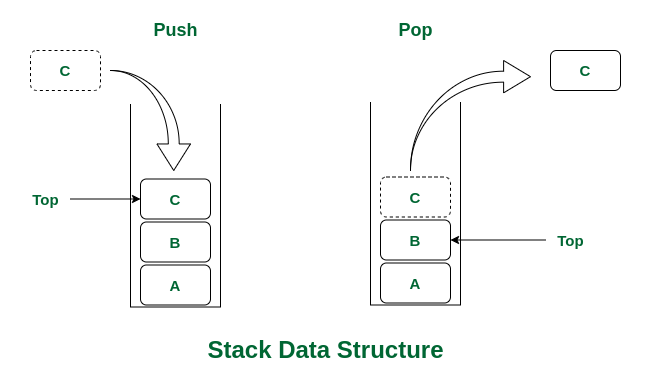
Stack là một cấu trúc dữ liệu dạng ngăn xếp (LIFO - Last In First Out), nó được sử dụng để lưu trữ các phần tử theo thứ tự cuối cùng vào đầu tiên ra (Last In First Out). 

Các phần tử được thêm vào và lấy ra khỏi stack thông qua hai thao tác cơ bản là push và pop. Khi thêm một phần tử mới vào stack thông qua phép toán push, phần tử này sẽ được đặt trên đỉnh của stack. Khi lấy ra một phần tử khỏi stack thông qua phép toán pop, phần tử ở đỉnh của stack sẽ bị loại bỏ và phần tử tiếp theo ở đáy của stack sẽ trở thành đỉnh của stack. 

Stack được sử dụng trong nhiều lĩnh vực như xử lý biểu thức toán học, đệ quy, quản lý bộ nhớ và nhiều ứng dụng khác.

2. Các phép toán cơ bản của Stack

• push(item): Thêm một phần tử vào đỉnh của stack.
• pop(): Lấy ra phần tử ở đỉnh của stack và xóa nó khỏi stack.
• peek(): Xem giá trị của phần tử ở đỉnh của stack mà không xóa nó khỏi stack.
• isEmpty(): Kiểm tra xem stack có rỗng hay không. Trả về True nếu stack rỗng, False nếu ngược lại.

#define MAX_SIZE 100

typedef struct {
    int items[MAX_SIZE];
    int top;
} Stack;

//Thêm một phần tử vào đỉnh của stack.

void push(Stack *s, int item) {
    if (s->top < MAX_SIZE - 1) {
        s->top++;
        s->items[s->top] = item;
    } else {
        printf("Stack overflow\n");
    }
}

//Lấy ra phần tử ở đỉnh của stack và xóa nó khỏi stack.

int pop(Stack *s) {
    int item;
    if (s->top >= 0) {
        item = s->items[s->top];
        s->top--;
        return item;
    } else {
        printf("Stack underflow\n");
        return -1;
    }
}

//Xem giá trị của phần tử ở đỉnh của stack mà không xóa nó khỏi stack.

int peek(Stack *s) {
    if (s->top >= 0) {
        return s->items[s->top];
    } else {
        printf("Stack is empty\n");
        return -1;
    }
}

//Kiểm tra xem stack có rỗng hay không. Trả về True nếu stack rỗng, False nếu ngược lại

int isEmpty(Stack *s) {
    return (s->top == -1);
}

//Hàm main để test các phương thức

int main() {
    Stack s;
    s.top = -1;

    push(&s, 1);
    push(&s, 2);
    push(&s, 3);

    printf("%d\n", pop(&s));
    printf("%d\n", peek(&s));

    return 0;
}

3. Ví dụ về ứng dụng của Stack 

Ví dụ về ứng dụng của Stack trong ngôn ngữ lập trình C: đảo ngược một chuỗi ký tự bằng cách sử dụng Stack. Ý tưởng của giải pháp là sử dụng Stack để lưu trữ các ký tự của chuỗi. Chúng ta sẽ đọc chuỗi từ trái sang phải và thêm các ký tự vào Stack. Sau đó, chúng ta lấy các ký tự ra khỏi Stack để tạo ra chuỗi ký tự đảo ngược.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_SIZE 100

typedef struct {
    char items[MAX_SIZE];
    int top;
} Stack;

void push(Stack *s, char item) {
    if (s->top < MAX_SIZE - 1) {
        s->top++;
        s->items[s->top] = item;
    } else {
        printf("Stack overflow\n");
    }
}

char pop(Stack *s) {
    char item;
    if (s->top >= 0) {
        item = s->items[s->top];
        s->top--;
        return item;
    } else {
        printf("Stack underflow\n");
        return '\0';
    }
}

int main() {
    char str[MAX_SIZE];
    printf("Enter a string: ");
    scanf("%s", str);

    Stack s;
    s.top = -1;

    // Push characters of the string onto the stack
    for (int i = 0; i < strlen(str); i++) {
        push(&s, str[i]);
    }

    // Pop characters from the stack to create the reversed string
    char reversed[MAX_SIZE];
    int i = 0;
    while (s.top >= 0) {
        reversed[i] = pop(&s);
        i++;
    }
    reversed[i] = '\0';

    printf("Reversed string: %s\n", reversed);

    return 0;
}
Trong đó, chúng ta định nghĩa kiểu dữ liệu Stack bằng cách sử dụng một struct, trong đó có một mảng các ký tự và một biến top để lưu trữ chỉ số của ký tự trên đỉnh của stack. Các phép toán push() và pop() được hiện thực bằng các hàm tương ứng.

4. Một số bài tập về Stack

1. Kiểm tra tính hợp lệ của một biểu thức toán học (bao gồm cả ngoặc đơn và ngoặc kép).
2. Chuyển đổi một biểu thức trung tố sang hậu tố và tính giá trị của biểu thức đó.
3. Chuyển đổi một biểu thức trung tố sang tiền tố và tính giá trị của biểu thức đó.
4. Sử dụng Stack để xử lý các bài toán liên quan đến các thuật toán duyệt đồ thị như DFS (Duyệt đồ thị theo chiều sâu) và BFS (Duyệt đồ thị theo chiều rộng).
5. Sử dụng Stack để đảo ngược một chuỗi kí tự hoặc một danh sách liên kết.
6. Xác định nếu một xâu kí tự là một Palindrome bằng cách sử dụng Stack.
7. Tìm tất cả các cặp số trong một mảng sao cho số đầu tiên nhỏ hơn số thứ hai, sử dụng Stack.
8. Sử dụng Stack để sắp xếp một danh sách các số nguyên theo thứ tự giảm dần.
9. Sử dụng Stack để tìm số lớn nhất trong một danh sách các số nguyên.
10. Sử dụng Stack để kiểm tra xem các dấu ngoặc đơn và ngoặc kép trong một biểu thức toán học có hợp lệ hay không.
11. Đảo ngược một chuỗi bằng cách sử dụng Stack.
12. Tính giá trị của một biểu thức toán học sử dụng Stack.
13. Tìm kiếm và xóa tất cả các phần tử trùng lặp trong một danh sách sử dụng Stack.
14. Chuyển đổi một biểu thức trung tố thành hậu tố sử dụng Stack.
15. Kiểm tra xem một dãy số có tăng dần hay không sử dụng Stack.